Dalil Segmen Garis pada Masalah Geometri dan Contoh Soalnya
Garis AB adalah himpunan tak terbatas dari titik-titik yang membentang tampa henti di kedua arah, tetapi satu baris. Sedangkan segmen garis AB adalah bagian dari garis AB dan memiliki panjang terbatas (titik A dan B sebagai batas)
Dalil segmen garis adalah:
Dalil 1 : (Sifat kongruen segmen garis)
Sifat kongruen segmen garis adalah refleksi, simetri dan transitif
Refleksi: Untuk setiap garis AB berlaku AB ≡ AB
Simetri : Jika AB ≡ CD, maka CD ≡ AB
Transitif : Jika AB ≡ CD, dan CD ≡ EF maka AB ≡ EF
Dalil 4 : Dua garis tidak berpotongan pada lebih dari satu titik
Pada gambar di dibawah
AEB dan CED berpotongan di titik D dan tidak berpotongan dititik lain.
Dalil 5 : Jika terdapat sebuah titik pada suatu garis hanya dapat dibuat satu garis tegak lurus melalui garis tersebut
Dalil 6 : Untuk setiap dua titik berbeda, hanya ada satu bilangan real positif, yaitu panjang segmen garis yang menghubungkan dua titik.
Pada gambar diatas, untuk titik A dan B yang berbeda, hanya ada satu bilangan real positif, diwakili oleh AB yang merupakan AB . yang merupakan jarak titik A ke titik B
Dalil 7 : Jarak terpendek antara dua titik adalah panjang ruas garis yang menghubungkan dua titik itu.
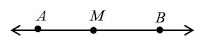
Dalil 8 : Segmen garis memiliki satu dan hanya satu titik tengah.
Pada gambar diatas, segmen AB memiliki titik tengah M, dan tidak ada titik tengah lain pada AB .
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
Penerapan dalil segmen garis adalah pada segitiga. Dalil yang berlaku pada segitiga adalah dalil titik tengah dan dalil intersept. Lebih lanjutnya bisa dilihat disini.
Pengembangan dari dalil intersept adalah apabila terdapat tiga garis sejajar dan ketiga garis itu dipotong oleh dua garis yang berpotongan, seperti tampak pada gambar dibawah, maka berlaku perbandingan
Contoh Soal
1. Pada segitiga ABC, D, E dan F masing-masing titik tengah AB, AC dan BC, dimana BC = 130 cm dan DF = 50 cm. Jika keliling segitiga ABC 340 cm, tentukanlah panjang EF
Jawab :
BC = 130 cm
DF = 50 cm maka AC = 2(50) = 100 cm
AB + BC + AC = 340
AB + 130 + 100 = 340
AB + 230 = 340 Jadi AB = 110 cm
Sehingga : EF = ½ AB = ½ (110) = 55 cm
2. Perhatikan gambar di bawah ini!
Jika panjang AC = 20 cm, BF = 4 cm, DF = 3,5 cm dan AB = 16 cm. Hitunglah panjang FG, DE, dan AD!
Jawab :
Untuk mencari panjang FG gunakan perbandingan ∆BFG dengan ∆ABC, maka diperoleh:
AB:BF = AC:FG
Atau
AB/BF = AC/FG
16 cm/4 cm = 20 cm/FG
16 cm . FG = 20 cm . 4 cm
FG = 20 cm . 4 cm/16 cm
FG = 5 cm
Jadi panjang FG adalah 5 cm
Sekarang cari panjang DE dengan menggunakan perbandingan ∆BDE dengan ∆ABC, maka diperoleh:
DE : AC = BD:AB
atau
DE/AC=BD/AB (dalam hal ini BD = BF+DF = 7,5 cm)
DE/20 cm = 7,5 cm/16 cm
DE = 20 cm . 7,5 cm/16 cm
DE = 9,375 cm
Jadi panjang DE adalah 9,375 cm
Sekarang cari panjang AD dengan menggunakan konsep penjumlahan, yakni:
AB = AD + DF + BFAB = AD + BD
AD = AB – BD
AD = 16 cm – 7,5 cm
AD = 8,5 cm
Jadi panjang AD adalah 8,5 cm.
3. Perhatikan gambar di bawah ini
Tentukan panjang OM dan ON pada gambar di atas!
Jawab :
OM = √(MP.MN)
OM = √(3 cm.12 cm)
OM = √(36 cm²)
OM = 6 cm
ON = √(NP.MN)
ON = √(9 cm.12 cm)
ON = √(108 cm²)
ON = √(36.3 cm²)
ON = 6√3 cm
Jadi panjang OM dan ON adalah 6 cm dan 6√3 cm.















Komentar
Posting Komentar